As this is still a work in progress, this is a storyboard. It is coarse, about 4 frames per second, and has a few typos to be corrected. It is a dynamic version of the ruler and compass construction that implements the transcendental function, gd(w). It’s a combination of synthetic and analytic geometry. The text boxes read out the trig projections at the current value of rapidity, the independent variable. It is twice the blue area bounded by the hyperbola. The red area bounded by the circle is half the gudermannian, or hypercomplex phase angle. Every point in the red area maps to a point in the blue area, and the edges map to the corresponding edges. The black lines are the axes, the gray line is the asymptote of the hyperbola. The unit circle is white and the unit hyperbola is magenta. The light blue arc is a portion of a circle whose radius is the hypotenuse of the right triangle, in yellow, formed by an arbitrary point on the perpendicular at the unit step, in green.
In terms of physics, the point P[8] represents Proper velocity, or celerity, measured by the y coordinate. P[2] is the real projection of the hypotenuse, which is always c, the velocity in time. The hypotenuse is the time component of the 4-velocity, which I have labeled Hyperspeed, as it is actually the Pythagorean composite of real time velocity and Proper velocity. The gudermannian is the elevation angle of the hypotenuse, and it is the arctan of celerity/c. The cosine projection of the complex hypotenuse on itself is the radius of the white circle, c. The point where it intersects the circle, P[5], has two coordinates, points P[1] and P[4], which, if divided by c, are the cosine and sine of the elevation angle, which are 1/γ and β, where β is the fraction of c that is measured velocity and γ is the Lorentz factor for that velocity. By scribing the arc from P[8] to P[3] and constructing a horizontal line through P[8] and a vertical line through P[3], the two intersect at P[9]. Although these coordinates are defined by the gudermannian, the point itself is on the unit hyperbola. In hyperbolic coordinates, they are the 4-velocity, and the elements of the Lorentz transform matrix (multiplied by c) that boost a point from 0 to measured velocity. The invariant in this drawing is the semi-major axis of the hyperbola, the unit step, c. The point, P[6] is the slope of the radius vector from the hyperbola to the origin, and it is on the same horizontal line as the intersection point, P[5], which is the sine of the elevation, or c sin(θ) = c tanh(w). Similarly, the tan(θ), which is the sine projection of the hypotenuse is the same height as the sinh(w), or Proper velocity = c tan(θ) = c sinh(w). The horizontal coordinate of P[9] and P[3] is the cosh(w) and the sec(θ), which is the Lorentz factor. The point P[8] is mislabeled. While the y component is the sinh, r is the hypotenuse, and it is the cosh, not the sinh. P[9] should be labeled 4-velocity.
From the nature of the construction, moving any one of the 4 points P[9], P[8], P[6] or P[5] forces a redetermination of all three of the others. Although we selected P[8] as the independent Proper velocity, as c sinh(w), all 4 points are unique functions of all the others, and any 1 of them can be used as the independent variable. However, of all the variables that can refer to velocity, rapidity is the only one that combines by linear addition, making it the most suitable as a hyperbolic coordinate and independent variable. If we scale the drawing by mass, point P[9] has the coordinates of 4-momentum, while P[8] has total relativistic momentum and the relativistic invariant for 4-momentum as its coordinates. The other horizontal line through P[5] and P[6] is the Newtonian momentum, the real, cosine projection of relativistic momentum. If we scale the same drawing by c again, the hypotenuse’ magnitude becomes total relativistic energy, while the radius to the white circle is rest energy and the remaining yellow portion is the relativistic kinetic energy. The three sides of the triangle represent the energy-momentum relationship, E²-c²p² = (mc²)². Of course, because the elevation angle is the gudermannian of the rapidity. This is also the definition of the horizontal hyperbola, where E is the horizontal coordinate, cp is the vertical coordinate and mc² is the semi-major axis, the invariant.
We can clearly see that as the Proper velocity goes to infinity, the elevation angle goes to 90 degrees. However, the cosine projection of the Proper velocity never makes it to the white circle, and the cosine projection of the hypotenuse onto itself never leaves the white circle. The white circle maxes out at an elevation angle of 90 degrees, when v=c and Proper velocity is infinite. Since momentum is based on the Proper velocity, not the measured velocity, it is also clear that c is not the ultimate limiting speed, since it is mapped to infinite Proper velocity. It is the limit of the observable cosine projections of Proper velocity, and we can’t observe anything faster, because there is no Proper velocity greater than infinity to project it. And since infinity is the same everywhere, the observable limit of its cosine projections is also the same everywhere, and lightspeed is constant. At the other extreme, note that all Newtonian velocities are tightly grouped in the immediate proximity of P[2]. The 4 points which are quite distinct at higher velocities, are all degenerate on the unit step, with virtually zero area in the quadrilateral defined by the 4 points. Compared to c, all Newtonian velocities are essentially on the baseline, with no difference between measured velocity and Proper velocity.
Since all 6 circular trig functions and all 6 hyperbolic trig functions are related by closed 6-groups of transformations, knowing any 1 of the 12 uniquely determines the other 11 (up to sign). I believe it is illogical to deny the physical nature of Proper velocity. It breaks the light speed barrier. It goes to infinity. Just deal with it.
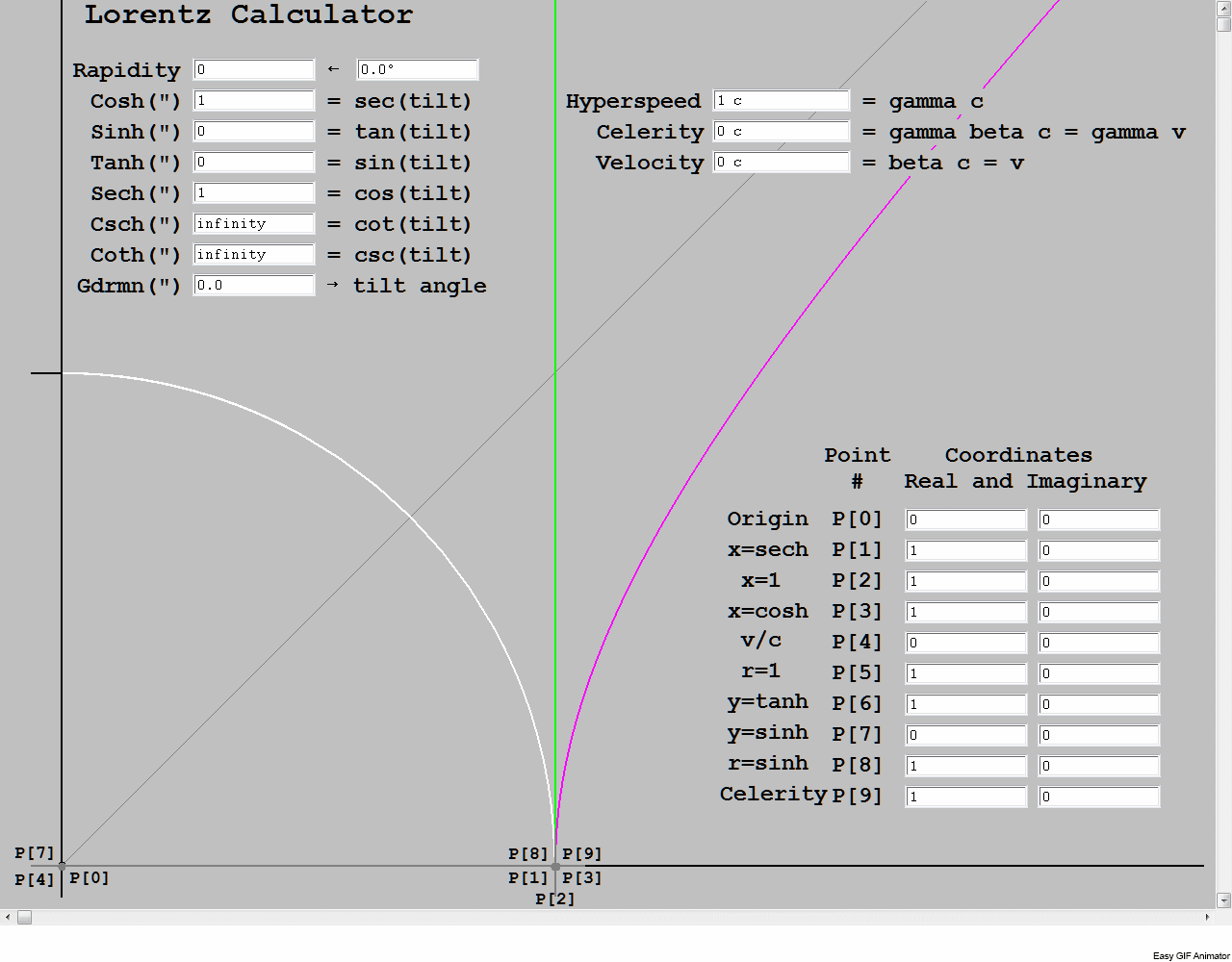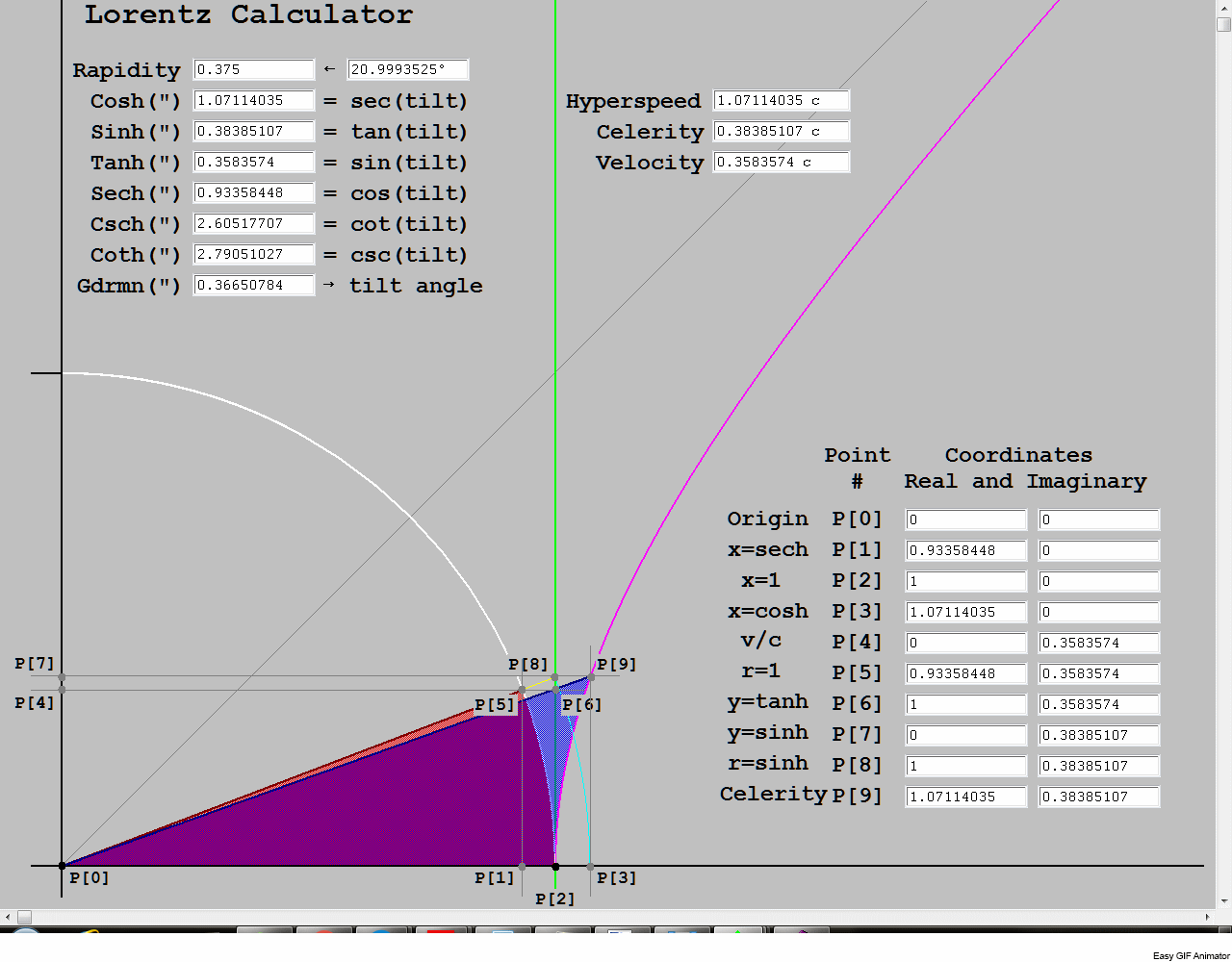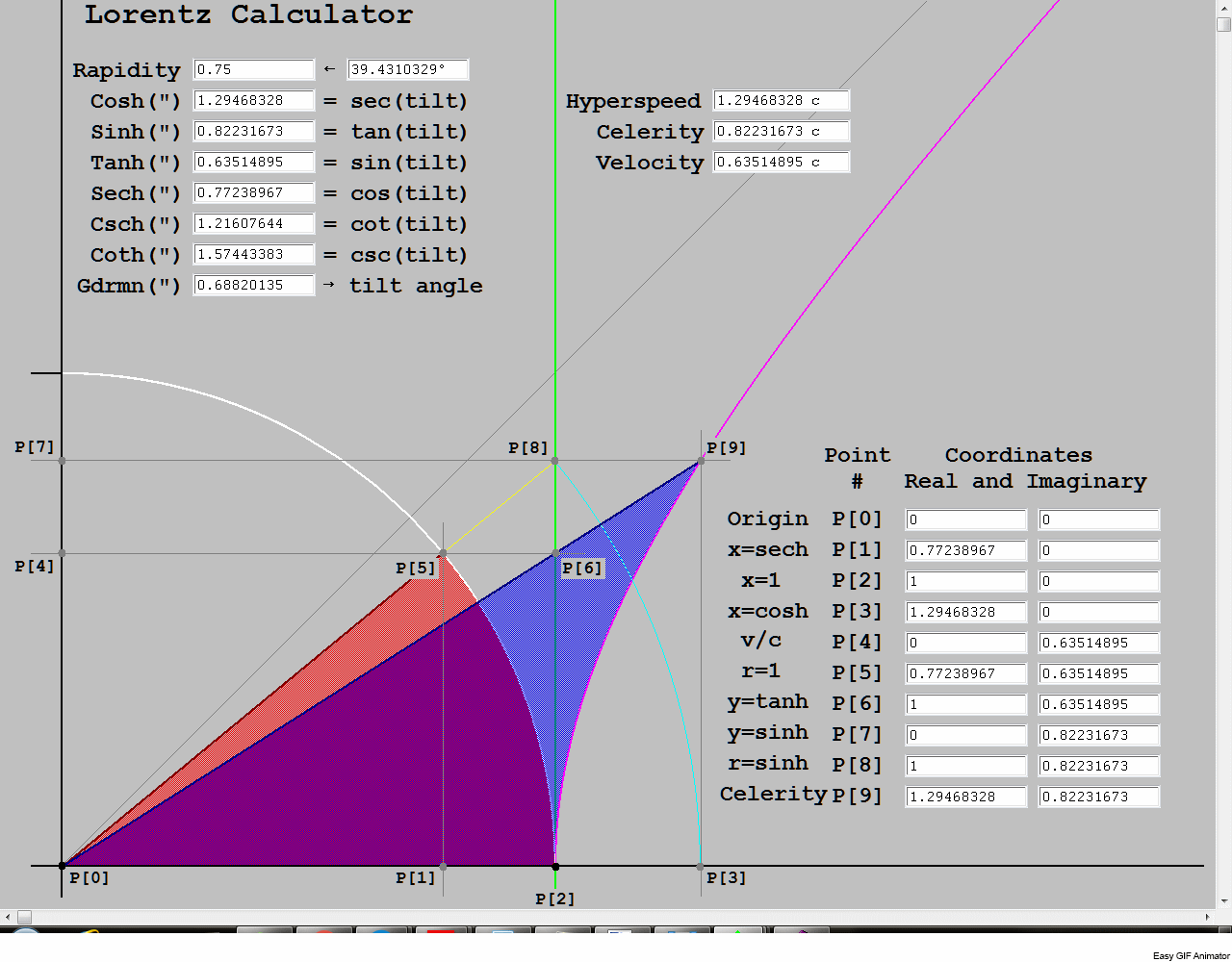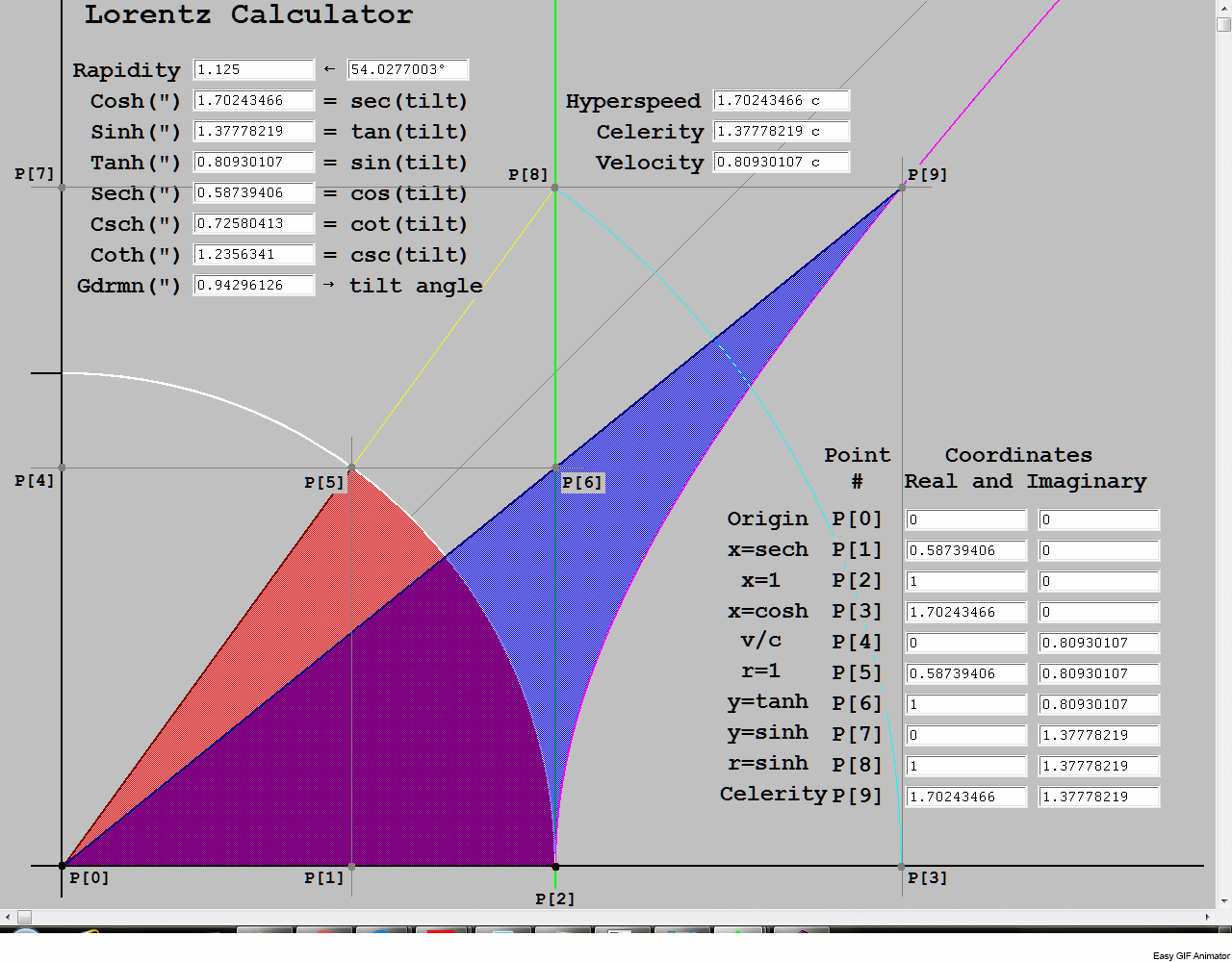
In this image, the variables, hyperbolic angle and circular angle, are represented by areas, not vectors. In the following images, the hyperbolic angle is represented as a dimension normal to the flat spacetime grid. Bivectors are frequently represented by such normals, but this conceals the 2 dimensional nature of the bivector, which has shape as an independent parameter besides magnitude, which is area. This is relevant to relativity, because both the hyperbolic magnitude and rotation angle are best represented as areas. Neither one has constant shape, but the magnitude has constant area as the shape changes from square to rectangle. The angle changes from 0 area to infinite area while the magnitude is invariant. The length of radius vectors is not relevant to bivectors. We will encounter this again when we discuss constant acceleration in hyperbolic coordinates. It has been demonstrated that there is an isomorphism in which rapidity is held constant, and changes in shape describe the accelerated coordinates.